How To Find The Centroid Of A Semicircle
Semicircle: how to summate perimeter, surface area, centroid, exercises
Content:
- Elements and measures of a semicircle
- Perimeter of a semicircle
- Area of a semicircle
- Centroid of a semicircle
- Moment of inertia of a semicircle
- Inscribed angle
- Solved exercises
- Exercise 1
- Solution
- Exercise 2
- Solution
- Exercise 3
- Solution
- Practice four
- Solution
- Exercise 5
- Solution
- References
The semicircle It is a flat figure delimited by a diameter of the circumference and 1 of the two flat circular arcs adamant by said diameter.
In this manner, a semicircle is bordered past a semicircumference, which consists of a flat circular arc and a direct segment that joins the ends of the flat circular arc. The semicircle encompasses the semicircle and all the points inside it.
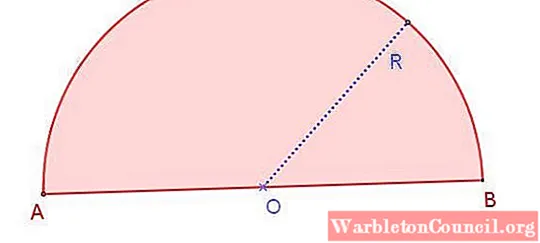
We tin see this in figure one, which shows a semicircle of radius R, whose mensurate is one-half that of diameter AB. Annotation that different a circle, in which in that location are infinite diameters, in the semicircle there is only one bore.
The semicircle is a geometric figure with many uses in architecture and design, as we run across in the following image:

Elements and measures of a semicircle
The elements of a semicircle are:
1.- The plane round arc A⌒B
two.- The segment [AB]
3.- The interior points to semicircle equanimous of the arc A⌒B and the segment [AB].
Perimeter of a semicircle
The perimeter is the sum of the contour of the arc plus that of the straight segment, therefore:
Perimeter = arc length A⌒B + segment length [AB]
In the case of a semicircle of radius R, its perimeter P will be given by the formula:
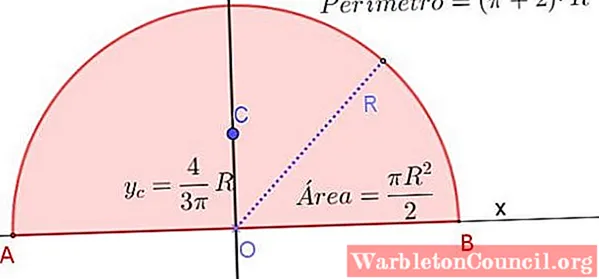
P = π⋅R + two⋅R = (π + 2) ⋅R
The first term is half the perimeter of a circle of radius R, while the 2nd is the length of the bore, which is twice the radius.
Area of a semicircle
Since a semicircle is one of the plane athwart sectors that remain when drawing a diameter through the circumference, its area A will be one-half the expanse of the circle that contains the semicircle of radius R:
A = (π⋅R2) / two = ½ π⋅R2
Centroid of a semicircle
The centroid of a semicircle is on its axis of symmetry at a summit measured from its diameter of iv / (3π) times the radius R.
This corresponds to approximately 0.424⋅R, measured from the center of the semicircle and on its axis of symmetry, every bit shown in Figure 3.
Moment of inertia of a semicircle
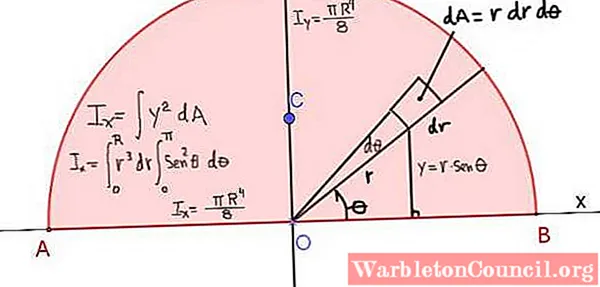
The moment of inertia of a plane figure with respect to an centrality, for instance ten axis, is defined as:
The integral of the foursquare of the distance of the points that belong to the figure to the axis, the integration differential being an infinitesimal chemical element of area, taken at the position of each indicate.
Figure 4 shows the definition of the moment of inertia Ix of the semicircle of radius R, with respect to the X axis that passes through its diagonal:
The moment of inertia about the x axis is given by:
Ix = (π⋅Riv) / viii
And the moment of inertia with respect to the axis of symmetry y is:
Iy = (π⋅R4) / 8
It is noted that both moments of inertia coincide in their formula, but it is of import to annotation that they refer to different axes.
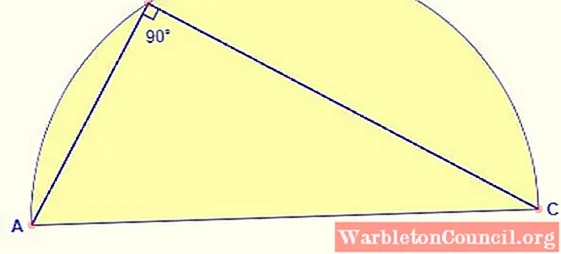
Inscribed angle
The angle inscribed in the semicircle is always 90º. Regardless of where the signal is taken on the arc, the angle betwixt sides AB and BC of the figure is always correct.

Solved exercises
Practise one
Decide the perimeter of a semicircle of radius x cm.
Solution
Remember that the perimeter every bit a function of the radius is given by the formula nosotros saw earlier:
P = (2 + π) ⋅R
P = (2 + iii.14) ⋅ 10 cm = 5.14 ⋅ 10 cm = 51.4 cm.
Exercise 2
Find the area of a semicircle with radius 10 cm.
Solution
The formula for the area of a semicircle is:
A = ½ π⋅R2 = ½ π⋅ (10cm)two = 50π cm2 = 50 x 3.14 cmii = 157 cm2.
Exercise 3
Determine the height h of the centroid of a semicircle of radius R = 10 cm measured from its base, the diameter of the semicircle being the same.
Solution
The centroid is the equilibrium point of the semicircle and its position is on the axis of symmetry at a pinnacle h from the base (bore of the semicircle):
h = (4⋅R) / (3π) = (4⋅10 cm) / (3 10 three.xiv) = 4.246 cm
Exercise 4
Find the moment of inertia of a semicircle with respect to the centrality that coincides with its diameter, knowing that the semicircle is made of a sparse sail. Its radius is ten cm and its mass is 100 grams.
Solution
The formula that gives the moment of inertia of the semicircle is:
Ix = (π⋅R4) / 8
Merely since the trouble tells us that information technology is a material semicircle, then the previous relationship must be multiplied by the surface density of mass of the semicircle, which will be denoted by σ.
Ix = σ (π⋅R4) / 8
We then continue to determine σ, which is zero other than the mass of the semicircle divided by its area.
The surface area was determined in practice ii and the result was 157 cmii. And then the surface density of this semicircle will be:
σ = 100 grams / 157 cmii = 0.637 chiliad / cmtwo
And then the moment of inertia with respect to the diameter will be calculated like this:
Ix = (0.637 thousand / cm2) [3.1416 ⋅ (10cm)4] / viii
Resulting:
Ix = 2502 g⋅cm2
Exercise 5
Determine the moment of inertia of a semicircle of radius 10 cm made of a material sheet with a surface density of 0.637 1000 / cm2 along an axis that passes through its centroid and is parallel to its diameter.
Solution
To solve this exercise it is necessary to remember Steiner's theorem on moments of inertia of parallel axes, which says:
The moment of inertia I with respect to an axis that is at a distance h from the centroid is equal to the sum of the moment of inertia Ic with respect to an axis that passes through the centroid and is parallel to the outset plus the product of the mass times the foursquare of the separation of the ii axes.
I = Ic+ Grand h2
In our case, I is known as the moment of inertia with respect to the diameter, which was already calculated in practise 4. The separation h between the diameter and the centroid is as well known, which was calculated in practice 3.
Nosotros merely take to clear Ic:
Ic = I - Thou htwo
Ic= 2502 grand⋅cm2 - 100g ⋅ (iv.246 cm)2 giving as a outcome that the moment of inertia through an axis parallel to the bore and passing through the centroid is:
Ic = 699.15 k⋅cm2
References
- Alexander, D. 2013. Geometry. 5th. Edition. Cengage Learning.
- Math Open Reference. Semicircle. Recovered from: mathopenref.com.
- Universe Formulas Semicircle. Recovered from: universoformulas.com.
- Universe Formulas. Expanse of a Semicircle. Recovered from: universoformulas.com.
- Wikipedia. Semicircle. Recovered from: en.wikipedia.com.
Source: https://warbletoncouncil.org/semicirculo-7039
Posted by: perezcardearty62.blogspot.com

0 Response to "How To Find The Centroid Of A Semicircle"
Post a Comment