How To Find The Coefficient Of Expansion

Learning Objectives

Past the end of this department, you will be able to:

• Define and describe thermal expansion.
• Calculate the linear expansion of an object given its initial length, change in temperature, and coefficient of linear expansion.
• Calculate the volume expansion of an object given its initial volume, change in temperature, and coefficient of volume expansion.
• Calculate thermal stress on an object given its original book, temperature alter, book change, and bulk modulus.

Figure 1. Thermal expansion joints similar these in the Auckland Harbour Bridge in New Zealand allow bridges to change length without buckling. (credit: Ingolfson, Wikimedia Commons)

The expansion of alcohol in a thermometer is one of many ordinarily encountered examples of thermal expansion, the change in size or volume of a given mass with temperature. Hot air rises because its book increases, which causes the hot air's density to exist smaller than the density of surrounding air, causing a buoyant (upward) force on the hot air. The same happens in all liquids and gases, driving natural rut transfer upwards in homes, oceans, and weather systems. Solids also undergo thermal expansion. Railroad tracks and bridges, for case, have expansion joints to allow them to freely expand and contract with temperature changes.

What are the basic properties of thermal expansion? First, thermal expansion is clearly related to temperature modify. The greater the temperature change, the more a bimetallic strip will bend. Second, it depends on the fabric. In a thermometer, for example, the expansion of alcohol is much greater than the expansion of the glass containing it.

What is the underlying crusade of thermal expansion? As is discussed in Kinetic Theory: Atomic and Molecular Explanation of Pressure level and Temperature, an increase in temperature implies an increment in the kinetic free energy of the individual atoms. In a solid, unlike in a gas, the atoms or molecules are closely packed together, but their kinetic energy (in the class of small, rapid vibrations) pushes neighboring atoms or molecules apart from each other. This neighbor-to-neighbor pushing results in a slightly greater distance, on boilerplate, between neighbors, and adds upward to a larger size for the whole body. For most substances under ordinary atmospheric condition, there is no preferred direction, and an increase in temperature will increment the solid'due south size past a certain fraction in each dimension.

Linear Thermal Expansion—Thermal Expansion in One Dimension

The change in length Δ50 is proportional to length L. The dependence of thermal expansion on temperature, substance, and length is summarized in the equation ΔFifty=αLΔT,where ΔL is the modify in length L, ΔT is the change in temperature, and α is the coefficient of linear expansion, which varies slightly with temperature.

Table 1 lists representative values of the coefficient of linear expansion, which may have units of ane/ºC or 1/G. Because the size of a kelvin and a degree Celsius are the same, both α and ΔT can be expressed in units of kelvins or degrees Celsius. The equation ΔFifty=αLΔT is authentic for small changes in temperature and tin exist used for large changes in temperature if an boilerplate value of α is used.

Tabular array 1. Thermal Expansion Coefficients at 20ºC[one]
Material	Coefficient of linear expansion α(1/ºC)	Coefficient of volume expansion β(i/ºC)
Solids
Aluminum	25 × x – 6	75 × x – 6
Brass	nineteen × 10 – half dozen	56 × 10 – 6
Copper	17 × 10 – 6	51 × x – half-dozen
Gilt	xiv × ten – six	42 × 10 – 6
Iron or Steel	12 × x – 6	35 × ten – 6
Invar (Nickel-iron alloy)	0.ix × 10 – 6	2.7 × x – half dozen
Lead	29 × 10 – 6	87 × 10 – 6
Silverish	18 × x – 6	54 × ten – vi
Glass (ordinary)	ix × 10 – six	27 × 10 – 6
Glass (Pyrex®)	3 × 10 – 6	9 × 10 – 6
Quartz	0.four × x – 6	1 × 10 – 6
Concrete, Brick	~12 × 10 – 6	~36 × x – half-dozen
Marble (average)	2.five × x – half-dozen	7.5 × 10 – 6
Liquids
Ether		1650 × x – six
Ethyl alcohol		1100 × 10 – 6
Petrol		950 × 10 – vi
Glycerin		500 × 10 – half-dozen
Mercury		180 × 10 – six
Water		210 × ten – 6
Gases
Air and nigh other gases at atmospheric pressure		3400 × 10 – 6

Example 1. Calculating Linear Thermal Expansion: The Golden Gate Bridge

The main span of San Francisco'south Gilt Gate Bridge is 1275 one thousand long at its coldest. The span is exposed to temperatures ranging from –15ºC to 40ºC. What is its alter in length between these temperatures? Assume that the bridge is fabricated entirely of steel.

Strategy

Employ the equation for linear thermal expansion ΔL =α 50ΔT to calculate the alter in length , ΔL. Employ the coefficient of linear expansion, α, for steel from Tabular array one, and annotation that the change in temperature, ΔT, is 55ºC.

Solution

Plug all of the known values into the equation to solve for ΔL.

[latex]\Delta{L}=\alpha{L}\Delta{L}=\left(\frac{12\times10^{-6}}{^{\circ}\text{C}}\right)\left(1275\text{ m}\right)\left(55^{\circ}\text{C}\right)=0.84\text{ yard}\\[/latex]

Word

Although not large compared with the length of the bridge, this change in length is observable. Information technology is generally spread over many expansion joints and so that the expansion at each articulation is small.

Thermal Expansion in Two and Three Dimensions

Objects expand in all dimensions, as illustrated in Figure ii. That is, their areas and volumes, likewise equally their lengths, increase with temperature. Holes too get larger with temperature. If you cutting a hole in a metal plate, the remaining material will expand exactly equally it would if the plug was still in place. The plug would get bigger, and so the hole must get bigger too. (Recollect of the ring of neighboring atoms or molecules on the wall of the hole equally pushing each other farther apart every bit temperature increases. Obviously, the ring of neighbors must get slightly larger, so the hole gets slightly larger).

Thermal Expansion in Ii Dimensions

For small temperature changes, the alter in area ΔA is given by ΔA= 2αAΔT, where ΔA is the change in expanse A, ΔT is the modify in temperature, and α is the coefficient of linear expansion, which varies slightly with temperature.

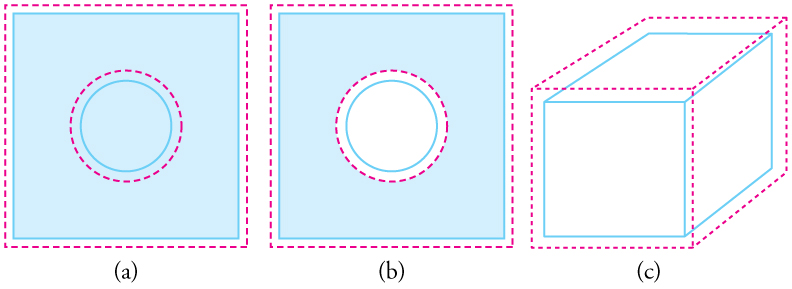
Figure 2. In general, objects expand in all directions as temperature increases. In these drawings, the original boundaries of the objects are shown with solid lines, and the expanded boundaries with dashed lines. (a) Area increases because both length and width increase. The surface area of a round plug as well increases. (b) If the plug is removed, the hole information technology leaves becomes larger with increasing temperature, just as if the expanding plug were still in identify. (c) Book also increases, considering all three dimensions increment.

Thermal Expansion in Three Dimensions

The alter in volume ΔV is very about ΔV = 3α VΔT. This equation is usually written every bit ΔV=βVΔT, where β is the coefficient of book expansion and β≈ 3α. Note that the values of β in Table 1 are about exactly equal to 3α.

In general, objects will aggrandize with increasing temperature. Water is the near important exception to this rule. Water expands with increasing temperature (its density decreases) when it is at temperatures greater than 4ºC (40ºF). However, it expands with decreasing temperature when it is between +4ºC and 0ºC (40ºF to 32ºF). Water is densest at +4ºC. (See Figure 3.) Perhaps the most striking upshot of this phenomenon is the freezing of water in a pond. When water nigh the surface cools down to 4ºC it is denser than the remaining water and thus will sink to the bottom. This "turnover" results in a layer of warmer water virtually the surface, which is then cooled. Eventually the swimming has a compatible temperature of 4ºC. If the temperature in the surface layer drops beneath 4ºC, the water is less dense than the water below, and thus stays near the top. Equally a upshot, the pond surface tin completely freeze over. The water ice on top of liquid h2o provides an insulating layer from winter's harsh exterior air temperatures. Fish and other aquatic life can survive in 4ºC h2o beneath ice, due to this unusual characteristic of water. It also produces apportionment of water in the pond that is necessary for a healthy ecosystem of the body of h2o.

Figure three. The density of water every bit a function of temperature. Note that the thermal expansion is actually very small-scale. The maximum density at +4ºC is only 0.0075% greater than the density at 2ºC, and 0.012% greater than that at 0ºC.

Making Connections: Real-Globe Connections—Filling the Tank

Figure four. Because the gas expands more the gas tank with increasing temperature, you tin can't bulldoze as many miles on "empty" in the summer every bit yous can in the wintertime. (credit: Hector Alejandro, Flickr)

Differences in the thermal expansion of materials can lead to interesting effects at the gas station. One example is the dripping of gasoline from a freshly filled tank on a hot mean solar day. Gasoline starts out at the temperature of the footing nether the gas station, which is cooler than the air temperature above. The gasoline cools the steel tank when it is filled. Both gasoline and steel tank expand as they warm to air temperature, only gasoline expands much more than steel, so information technology may overflow.

This difference in expansion can also cause problems when interpreting the gasoline gauge. The actual amount (mass) of gasoline left in the tank when the judge hits "empty" is a lot less in the summer than in the winter. The gasoline has the same volume every bit it does in the wintertime when the "add fuel" lite goes on, merely because the gasoline has expanded, there is less mass. If you are used to getting another twoscore miles on "empty" in the winter, beware—you will probably run out much more quickly in the summer.

Example 2. Calculating Thermal Expansion: Gas vs. Gas Tank

Suppose your 60.0-L (fifteen.ix-gal) steel gasoline tank is full of gas, so both the tank and the gasoline have a temperature of fifteen.0ºC. How much gasoline has spilled past the fourth dimension they warm to 35.0ºC?

Strategy

The tank and gasoline increment in volume, but the gasoline increases more than, and so the corporeality spilled is the difference in their book changes. (The gasoline tank can exist treated equally solid steel.) We can employ the equation for volume expansion to calculate the modify in book of the gasoline and of the tank.

Solution

1. Use the equation for volume expansion to summate the increase in volume of the steel tank: ΔV _s =β _southward V _southΔT.
2. The increase in book of the gasoline is given by this equation: ΔV _gas =β _gas V _gasΔT.
3. Find the departure in volume to determine the amount spilled as5 _spill=Δ5 _gas − ΔFive _s.

Alternatively, we can combine these 3 equations into a single equation. (Note that the original volumes are equal.)

[latex]\begin{array}{lll}{5}_{\text{spill}}& =& \left({\beta }_{\text{gas}}-{\beta }_{\text{due south}}\correct)V\Delta T\\ & =& \left[\left(\text{950}-\text{35}\right)\times {\text{10}}^{-half dozen}/^{\circ}\text{C}\right]\left(\text{60}\text{.}0\text{L}\correct)\left(\text{xx}\text{.}0^{\circ}\text{C}\correct)\\ & =& 1\text{.}\text{10}\text{L}\end{assortment}\\[/latex]

Word

This amount is significant, particularly for a 60.0-L tank. The upshot is so hitting because the gasoline and steel aggrandize quickly. The rate of change in thermal backdrop is discussed in the chapter Heat and Heat Transfer Methods.

If you try to cap the tank tightly to prevent overflow, you lot will notice that information technology leaks anyway, either around the cap or by bursting the tank. Tightly constricting the expanding gas is equivalent to compressing it, and both liquids and solids resist being compressed with extremely large forces. To avoid rupturing rigid containers, these containers take air gaps, which allow them to expand and contract without stressing them.

Thermal Stress

Thermal stress is created by thermal expansion or contraction (see Elasticity: Stress and Strain for a discussion of stress and strain). Thermal stress can exist destructive, such as when expanding gasoline ruptures a tank. Information technology can also be useful, for case, when ii parts are joined together past heating 1 in manufacturing, then slipping it over the other and allowing the combination to cool. Thermal stress can explain many phenomena, such as the weathering of rocks and pavement by the expansion of ice when it freezes.

Example 3. Calculating Thermal Stress: Gas Pressure

What pressure would be created in the gasoline tank considered in Example 2, if the gasoline increases in temperature from 15.0ºC to 35.0ºC without beingness allowed to expand? Assume that the majority modulus B for gasoline is one.00 × 10⁹ North/m².

Strategy

To solve this problem, we must apply the post-obit equation, which relates a change in book ΔV to force per unit area:

[latex]\Delta{V}=\frac{1}{B}\frac{F}{A}V_0\\[/latex]

where [latex]\frac{F}{A}\\[/latex] is pressure, V ₀ is the original volume, and B is the bulk modulus of the material involved. We will use the amount spilled in Example 2 as the modify in volume, ΔFive.

Solution

1. Rearrange the equation for calculating pressure: [latex]P=\frac{F}{A}=\frac{\Delta{V}}{V_0}B\\[/latex].
2. Insert the known values. The bulk modulus for gasoline is B = 1.00 × 10⁹ N/m². In the previous instance, the change in book ΔV = ane.10 L is the amount that would spill. Here, V ₀ = 60.0 L is the original book of the gasoline. Substituting these values into the equation, nosotros obtain [latex]P=\frac{ane.x\text{ L}}{60.0\text{ Fifty}}\left(i.00\times10^9\text{ Pa}\right)=i.83\times10^7\text{ Pa}\\[/latex].

Discussion

This pressure is about 2500 lb/in^two, much more than a gasoline tank tin can handle.

Forces and pressures created by thermal stress are typically every bit great as that in the case above. Railroad tracks and roadways can buckle on hot days if they lack sufficient expansion joints. (See Figure 5.) Power lines sag more than in the summer than in the winter, and will snap in cold weather if in that location is bereft slack. Cracks open and close in plaster walls every bit a house warms and cools. Glass cooking pans will crack if cooled rapidly or unevenly, considering of differential contraction and the stresses it creates. (Pyrex® is less susceptible because of its small coefficient of thermal expansion.) Nuclear reactor force per unit area vessels are threatened by overly rapid cooling, and although none accept failed, several have been cooled faster than considered desirable. Biological cells are ruptured when foods are frozen, detracting from their taste. Repeated thawing and freezing accentuate the damage. Even the oceans tin can exist afflicted. A significant portion of the ascent in body of water level that is resulting from global warming is due to the thermal expansion of sea h2o.

Effigy 5. Thermal stress contributes to the germination of potholes. (credit: Editor5807, Wikimedia Commons)

Metal is regularly used in the human trunk for hip and knee joint implants. About implants need to exist replaced over time because, among other things, metal does not bail with os. Researchers are trying to find better metal coatings that would allow metallic-to-bone bonding. One challenge is to observe a coating that has an expansion coefficient similar to that of metallic. If the expansion coefficients are as well different, the thermal stresses during the manufacturing procedure atomic number 82 to cracks at the coating-metal interface.

Some other case of thermal stress is found in the mouth. Dental fillings tin can expand differently from tooth enamel. It can requite pain when eating ice cream or having a hot drink. Cracks might occur in the filling. Metal fillings (golden, silver, etc.) are existence replaced by blended fillings (porcelain), which take smaller coefficients of expansion, and are closer to those of teeth.

Check Your Understanding

Two blocks, A and B, are made of the same material. Block A has dimensions l×due west×h=L× 2L×L and Block B has dimensions 250× two50× 2L. If the temperature changes, what is

1. the change in the book of the two blocks,
2. the change in the cross-exclusive area l×w, and
3. the change in the height h of the two blocks?

Figure half dozen.

Solution

1. The change in volume is proportional to the original volume. Block A has a book of 50× 2Fifty×L= 2L ³.Block B has a volume of 2L× 2L× twoL= 8L ³ , which is 4 times that of Block A. Thus the alter in volume of Block B should exist 4 times the change in volume of Block A.
2. The modify in expanse is proportional to the surface area. The cross-sectional area of Block A is L× 2Fifty= 2Fifty ⁱⁱ , while that of Block B is ii50× twoL= 4L ². Because cantankerous-sectional area of Block B is twice that of Block A, the alter in the cross-sectional area of Block B is twice that of Block A.
3. The change in height is proportional to the original height. Because the original height of Block B is twice that of A, the alter in the height of Block B is twice that of Block A.

Section Summary

• Thermal expansion is the increase, or subtract, of the size (length, area, or book) of a torso due to a change in temperature.
• Thermal expansion is large for gases, and relatively pocket-size, only non negligible, for liquids and solids.
• Linear thermal expansion is ΔL= αLΔT, where ΔL is the change in length L, ΔT is the modify in temperature, and α is the coefficient of linear expansion, which varies slightly with temperature.
• The alter in surface area due to thermal expansion is ΔA= 2αAΔT, where ΔA is the change in area.
• The change in volume due to thermal expansion is Δ5= βVΔT, where β is the coefficient of book expansion and β≈ 3α. Thermal stress is created when thermal expansion is constrained.

Conceptual Questions

1. Thermal stresses caused past uneven cooling can hands pause drinking glass cookware. Explain why Pyrex®, a glass with a small coefficient of linear expansion, is less susceptible.
2. Water expands significantly when it freezes: a volume increment of virtually 9% occurs. Equally a result of this expansion and because of the germination and growth of crystals as water freezes, anywhere from 10% to 30% of biological cells are flare-up when animal or establish cloth is frozen. Hash out the implications of this jail cell harm for the prospect of preserving human bodies by freezing and then that they tin can be thawed at some future date when it is hoped that all diseases are curable.
3. One method of getting a tight fit, say of a metallic peg in a hole in a metal cake, is to manufacture the peg slightly larger than the hole. The peg is then inserted when at a different temperature than the cake. Should the block exist hotter or colder than the peg during insertion? Explicate your answer.
4. Does information technology really help to run hot water over a tight metal lid on a drinking glass jar before trying to open it? Explicate your respond.
5. Liquids and solids expand with increasing temperature, considering the kinetic energy of a torso'southward atoms and molecules increases. Explain why some materials shrink with increasing temperature.

Problems & Exercises

1. The height of the Washington Monument is measured to exist 170 1000 on a solar day when the temperature is 35 . 0 º C . What volition its height exist on a twenty-four hour period when the temperature falls to – ten . 0 º C ? Although the monument is made of limestone, assume that its thermal coefficient of expansion is the same as marble's.
2. How much taller does the Eiffel Belfry get at the stop of a day when the temperature has increased past xv º C ? Its original height is 321 k and you can presume it is fabricated of steel.
3. What is the modify in length of a 3.00-cm-long column of mercury if its temperature changes from 37 . 0 º C to xl . 0 º C , assuming the mercury is unconstrained?
4. How big an expansion gap should be left between steel railroad rails if they may reach a maximum temperature 35.0ºC greater than when they were laid? Their original length is 10.0 m.
5. You are looking to purchase a small piece of state in Hong Kong. The cost is "simply" $threescore,000 per square meter! The country title says the dimensions are 20 one thousand × 30 g. Past how much would the total price change if you measured the parcel with a steel tape measure on a day when the temperature was 20ºC above normal?
6. Global warming will produce rising body of water levels partly due to melting ice caps but besides due to the expansion of water as average ocean temperatures rising. To get some idea of the size of this effect, calculate the change in length of a cavalcade of water one.00 km high for a temperature increase of ane.00ºC. Note that this calculation is only guess considering ocean warming is not compatible with depth.
7. Show that 60.0 50 of gasoline originally at 15.0ºC will expand to 61.one L when it warms to 35.0ºC, as claimed in Example 2.
8. (a) Suppose a meter stick made of steel and one made of invar (an blend of iron and nickel) are the aforementioned length at 0ºC. What is their difference in length at 22.0ºC? (b) Repeat the calculation for two xxx.0-m-long surveyor's tapes.
9. (a) If a 500-mL drinking glass beaker is filled to the brim with ethyl alcohol at a temperature of 5.00ºC, how much will overflow when its temperature reaches 22.0ºC? (b) How much less water would overflow under the aforementioned conditions?
10. About automobiles have a coolant reservoir to take hold of radiator fluid that may overflow when the engine is hot. A radiator is made of copper and is filled to its xvi.0-Fifty capacity when at 10.0ºC. What volume of radiator fluid will overflow when the radiator and fluid accomplish their 95.0ºC operating temperature, given that the fluid's volume coefficient of expansion is β= 400 × 10^–vi/ºC? Note that this coefficient is approximate, because nearly car radiators accept operating temperatures of greater than 95.0ºC.
11. A physicist makes a cup of instant coffee and notices that, as the coffee cools, its level drops 3.00 mm in the glass cup. Show that this subtract cannot be due to thermal contraction by calculating the decrease in level if the 350cm3 of coffee is in a 7.00-cm-diameter cup and decreases in temperature from 95.0ºC to 45.0ºC. (Nearly of the drib in level is actually due to escaping bubbles of air.)
12. (a) The density of h2o at 0ºC is very nearly 1000kg/m3 (information technology is actually 999.84 kg/1000^three), whereas the density of ice at 0ºC is 917 kg/chiliad³. Calculate the pressure necessary to keep ice from expanding when it freezes, neglecting the effect such a large force per unit area would have on the freezing temperature. (This problem gives you simply an indication of how large the forces associated with freezing water might be.) (b) What are the implications of this result for biological cells that are frozen?
13. Show that β ≈ 3α, by calculating the change in book ΔV of a cube with sides of length L.

Glossary

thermal expansion: the change in size or volume of an object with alter in temperature

coefficient of linear expansion: α, the change in length, per unit of measurement length, per 1ºC modify in temperature; a constant used in the adding of linear expansion; the coefficient of linear expansion depends on the fabric and to some degree on the temperature of the fabric

coefficient of volume expansion:β, the change in volume, per unit volume, per 1ºC change in temperature

thermal stress: stress caused past thermal expansion or contraction

Selected Answers to Bug & Exercises

1. 169.98 m

3. 5.4 × 10^{−half dozen} m

five. Because the area gets smaller, the price of the land DECREASES by ~$17,000.

seven. [latex]\begin{array}{lll}V& =& {V}_{0}+\Delta V={Five}_{0}\left(1+\beta \Delta T\correct)\\ & =& \left(\text{60}\text{.}\text{00 L}\correct)\left[i+\left(\text{950}\times {\text{ten}}^{-6}/^{\circ}\text{C}\right)\left(\text{35}\text{.}0^{\circ}\text{C}-\text{15}\text{.}0^{\circ}\text{C}\right)\correct]\\ & =& \text{61}\text{.}1\text{L}\end{array}\\[/latex]

9. (a) nine.35 mL; (b) 7.56 mL

11. 0.832 mm

13. We know how the length changes with temperature: ΔL= αL ₀ΔT. As well we know that the volume of a cube is related to its length past Five= Fifty ^three, so the final book is and so V= Five ₀+ ΔV= (L ₀ + Δ50)³. Substituting for ΔL givesV= (L ₀ + αFifty ₀ΔT)³= Fifty₀ ³(1 + αΔT)ⁱⁱⁱ.

Now, because αΔT is pocket-size, we can use the binomial expansion:5≈ L ₀ ³(i + 3αΔT) = L ₀ ^three+ 3α50 ₀ ³ΔT.

So writing the length terms in terms of volumes gives Five= 5 ₀+ ΔFive≈ Five ₀+ 3αV ₀ΔT, and so ΔV=βV ₀ΔT≈ 3αV ₀ΔT, or β≈ 3α.

---

Source: https://courses.lumenlearning.com/physics/chapter/13-2-thermal-expansion-of-solids-and-liquids/#:~:text=The%20dependence%20of%20thermal%20expansion,which%20varies%20slightly%20with%20temperature.

Posted by: perezcardearty62.blogspot.com

Share this post